A correlation requires at least 2 continuous variables. We need to first define our variables in Variable View. In this case, we’re looking at how number of absences relates to grade point average.
Next, we type in our data points in Data View.
A regression can be seen as a kind of extension of a correlation. When doing a regression, you find a lot of the same outputs, like Pearson’s r and r-squared. The difference is that the point of a regression is to also construct a model (usually linear) that will help us predict values using a line of best fit. In the case of this example, we will be looking at average hours of sleep students get and comparing it to their GPA. A regression will also give us a model (y=mx+b) that would allow us to predict the GPA of a hypothetical student if we knew the average amount of sleep they get a night.
First, we need to create our variables in Variable View.
Then, we need to input our data into Data View. You can’t see it in this photo, but I have 25 participants total. Continue reading
Many statistical tests run on the assumption that the data with which you are working is normally distributed, so it’s important to check. There are several different ways to go about this,. This post will explain a few different methods for testing normalcy as well as provide some instructions about how to run these tests in Excel.
An important rule to note about distribution is that in a normal distribution, the mean, median, and mode are approximately equal. What it looks like visually is that the mean, median, and mode are all sitting at the top of the hump of the bell curve. When a distribution is skewed, these values become different. The mode will always sit around the hump of a distribution (because this is where most of the values have accumulated). The mean is the measure of central tendency most affected by extreme variables and outliers, so it will follow the longest tail. The median, in this case, will always fall somewhere between the median and the mode. Put another way, if the distribution is positively skewed, the mean will be the greatest value, the median will be the second greatest value, and the mode will be the smallest value. If the distribution is negatively skewed, the mean will be the smallest value, the median will be the second smallest value, and the mode will be the greatest value. So when you’re looking at a data set, you may be able to get an idea of the skew of the distribution by comparing the mean and the median.
A set is a collection of objects of values that are in this case called elements or members. They can be described using words, lists, or set-builder notation.
If a set has no elements, it’s called an empty or null set and its symbol is Ø. Make sure not to write this as {Ø}, because that is technically incorrect.
It is important to make sure that a set is well-defined, meaning that there’s no room for subjective interpretation about whether something belongs in a set or not. An example of a well-defined set is a set of all numbers between 1 and 10. We can say for sure that 5 belongs and 13 doesn’t. A set that is not well defined is a set of all numbers that are aesthetically pleasing. It’s not clear what would define aesthetically pleasing so we’re unsure about whether 5 or 13 would fit. Continue reading
Before we can talk about how to use inductive reasoning, we need to define it and distinguish it from deductive reasoning.
Inductive reasoning is when one makes generalizations based on repeated observations of specific examples. For instance, if I have only ever had mean math teachers, I might draw the conclusion that all math teachers are mean. Because I witnessed multiple instances of mean math teachers and only mean math teachers, I’ve drawn this conclusion. That being said, one of the downfalls of inductive reasoning is that it only takes meeting one nice math teacher for my original conclusion to be proven false. This is called a counterexample. Since inductive reasoning can so easily be proven false with one counterexample, we don’t say that a conclusion drawn from inductive reasoning is the absolute truth unless we can also prove it using deductive reasoning. With inductive reasoning, we can never be sure that what is true in a specific case will be true in general, but it is a way of making an educated guess.
Deductive reasoning depends on a hypothesis that is considered to be true. In other words, if X = Y and Y = Z, then we can deduce that X = Z. An example of this might be that if we know for a fact that all dogs are good, and Lucky is a dog, then we can deduce that Lucky is good. Continue reading
A rational number is a number that can be written as a quotient of integers. In other words, it’s any number that can create a nice and neat fraction. A rational expression is also a quotient, it’s just made up of polynomials. A rational expression can be written in the form P/Q. For example:
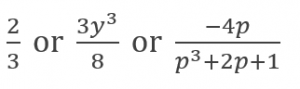
Rational expressions have different numerical values depending on what values replace the variables. For example:
Finding the greatest common factor simply involves finding the largest number or term which will fit evenly into each number or term in a list. The way I like to go about this is by breaking each number or term into its smallest parts. Break each number down until you are multiplying together only prime numbers. All the numbers that they have in common should then be multiplied back up to create the GCF.
This is what it would look like in a list of numbers:
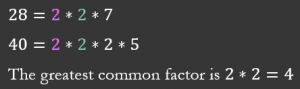
And this is what it would look like in a list of terms:
When working with exponents, it might be more helpful to think of them as multiple instances of multiplication. Some exponents are going to be more straight-forward, but be careful of the writing of some exponents.
Let’s take a look at some examples of evaluating exponential expressions:
In the expression below, this is an illustration of what we mean when we say that an exponent is like multiple multiplications. The exponents signify the number of times that the number 2 should be multiplied by itself.
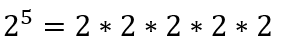
In the next expression, the -3 is in parentheses. This means that the exponent outside of the parentheses needs to be applied to the number as a whole, including its being negative.
Reading graphs of two-way ANOVAs is often a little frustrating at first for students who are new to reading them. The goal of this post is to hopefully make the process more straight-forward.
If you’re not sure already what a main effect or interaction is, I would suggest heading over to another post about two-way ANOVAs first. The purpose of one of these graphs is to help the reader visualize the results of the test when reading the results can sometimes be overwhelming, especially if the researchers are working with several different levels in each independent variable. The first trick to remember is that when looking for a significant main effect in the variable on the X-axis, we want the mean distance between the two points above one condition to be different from the mean distance between the two points of another condition. A clear example of this is below. The middle point between the orange line and blue line above “Little Sunlight” is around 2.8, while the middle point between the orange line and blue line above “Lots of Sunlight” is about 4.8. Given the context, we would say that there is a main effect for sunlight in which plant growth increases as levels of sunlight increase.
Just like an independent samples t-test, an Independent measures one-way ANOVA uses independent subjects for each level/condition within an independent variable. In this example, we’re growing plants. In Variable View, I’ve made the independent variable Condition (in this case the amount of water I’ll be giving to the plants) and the dependent variable Height.
