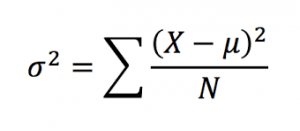Statistics: Probability and Sampling

Leave a reply

Introduction to Probability and Sampling

Probabilities

A probability is a fraction or a proportion of all the possible outcomes. So it’s the number of classified outcomes classified as X divided by the total number of possible outcomes (N). It’s generally reported as a decimal, but it can also be reported as a fraction or a percentage. 

What is the role of probability in populations, samples, and inferential statistics? As we discussed before, because it’s usually impossible for researchers to draw data from the entirety of a population, they draw samples. The size of the sample affects how comparable the sample population is to the general population. Probability is used to predict what kind of samples are likely to be obtained from a population. Thus, probability establishes a connection between samples and populations; we know from looking at the population how likely it is for a specific sample to be drawn. We also use proportions that exist within samples to infer the probabilities that exist within a population. Inferential statistics rely on this connection when they use sample data as the basis for making conclusions about populations. Continue reading →

Statistics: Z-score Basics

Leave a reply

Z-Score Introduction

Standardized Distributions

Sometimes when working with data sets, we want to have the scores on the distribution standardized. Essentially, this means that we convert scores from a distribution so that they fit into a model that can be used to compare and contrast distributions from different works. For example, if you have a distribution of scores that show the temperature each day over the summer in Boston, it may be recorded in Fahrenheit. Someone else in Paris may have recorded their summer temperatures as well but in Celcius. If we wanted to compare these distributions of scores based on their descriptive statistics, we may want to convert them to the same standardized unit of measurement. 

Standardized distributions have one single unit of measurement. Raw scores are transformed into this standardized unit of measurement to be compared to one another. Ultimately, they should look just like the original distribution, the only difference is that the scores have been placed on a different unit of measurement. Continue reading →

Statistics: Variability

Leave a reply

Basics of Variability

Variability is often a difficult topic for newcomers to statistics to grasp. Essentially it is the spread of the scores in a frequency distribution. If you have a bell curve which is pretty flat, you would say that it has high variability. If you have a bell curve which is pointy, you would say that it has low variability. Variability is really a quantitative measure of the differences between scores and describes the degree to which the score are spread out or clustered together. The purpose of measuring variability is to be able to describe the distribution and measure how well an individual score represents the distribution.

There are three main types of variability:

  • Range: The distance between the lowest and the highest score in a distribution. Can be described as one number or represented by writing out the lowest and highest number together (ex. values 4-10). Calculated by subtracting the highest score from the lowest score. If you’re working with continuous variables, it’s the upper real limit for Xmax minus the lower real limit for Xmin.
  • Standard deviation: The average distance between the scores in a data set and the mean. Here’s a video to help you conceptualize this. This value is also the square root of the variance.
  • Variance: Measures the average squared distance from the mean. This number is good for some calculations, but generally we want the standard deviation to determine how spread out a distribution is. Calculated with this equation:

Continue reading →

Statistics: Measures of Central Tendency

Leave a reply

Central Tendency

Central tendency is a statistical measure; a single score to define the center of a distribution. It is also used to find the single score that is most typical or best represents the entire group. No single measure is always best for both purposes. There are three main types:

  • Mean: sum of all scores divided by the number of scores in the data, also referred to as the average.
  • Median: the midpoint of the scores in a distribution when they are listen in order from smallest to largest. It divides the scores into two groups of equal size. With an even number of scores, you compute the average of the two middle scores.
  • Mode: the most frequently occurring number(s) in a data set.

Here are a variety of videos to help you understand the concepts of these measures, finding the median using a histogram, and finding a missing value given the mean. Continue reading →

Statistics: Frequency Distributions

Leave a reply

Frequency Distributions

In statistics, a lot of tests are run using many different points of data and it’s important to understand how those data are spread out and what their individual values are in comparison with other data points. A frequency distribution is just that – an outline of what the data look like as a unit. A frequency table is one way to go about this. It’s an organized tabulation showing the number of individuals located in each category on the scale of measurement. When used in a table, you are given each score from highest to lowest (X) and next to it the number of times that score appears in the data (f). A table in which one is able to read the scores that appear in a data set and how often those particular scores appear in the data set. Here’s a link to a Khan Academy video we found to be helpful in explaining this concept.

Organizing Data into a Frequency Distribution

  1. Find the range
  2. Order the table from highest score to lowest score, not skipping scores that might not have shown up in the data set.
  3. In the next column, document how many times this score shows up in the data set

Organizing data into a group frequency table

  1. The grouped frequency table should have about 10 intervals. A good strategy is to come up with some widths according to Guideline 2 and divide the total range of numbers by that width to see if there are close to 10 intervals.
  2. The width of the interval should be a relatively simple number (like 2, 5, or 10)
  3. The bottom score in each class interval should be a multiple of the width (0-9, 10-19, 20-19, etc.)
  4. All intervals should be the same width.

Continue reading →

Introduction to Statistics Basics

Leave a reply

Some Statistics Basics!

Whether this is your first statistics class or whether you’re just in need of a refresher, there are a few basic statistical principles which are necessary for one to understand before moving forward.

Understanding Populations and Samples

Populations are the groups of people that we are interested in studying. This can be the entirety of people with depression, an entire town, or dog-owners. Populations can vary in size but are typically very large. They are almost always impossible to study in their entirety. Therefore, we select samples from a population. Although they’re never as diverse as the population, they are generally representative. However, they provide limited information and introduce sampling error.

Samples are a subset of the population which as been selected by various means. A sample is representative when it accounts for the variability and diversity of the population. For example, a representative sample of “individuals who attend the University of Baltimore” would include a diversity of age groups, race, educational background, students from different programs, faculty from multiple departments, staff, etc., in their appropriate percentages in the population. A non-representative sample in that case would not account for the various differences that exist among the individuals in a population, or would over-represent/under-represent a specific group. The figure below illustrates a hypothetical population, two examples of non-representative samples, and one representative sample of that population. Continue reading →