Statistics: Regression

Leave a reply

Introduction to Linear Regression

Linear regression is a method for determining the best-fitting line through a set of data. In a lot of ways, it’s similar to a correlation since things like r and r squared are still used. The one difference is that the purpose of regression is prediction. The best-fitting line is calculated through the minimization of total squared error between the data points and the line.

The equation used for regression is Y = a +bx or some variation of that. If you remember from algebra class, this formula is like Y=mx+b. This is because they are both the linear equation. Although you may be asked to report r and r squared, the purpose of regression is to be able to find values for the slope (b) and the y-intercept (a) that creates a line that best fits through the data. Continue reading →

Statistics: Correlation

Leave a reply

Introduction to Correlation and Regression

So far we’ve been talking about analyses which involve variables which are split up into categorical or discrete variables (ex. treatment A, B, C) compared to a dependent variable which is continuous (ex. plant height). However, there is a way to look at two variables which have continuous data: correlation. A correlation will tell you the characteristics of a relationship such as direction (either positive or negative), form (we often work with linear relationships), and strength of the relationship. Strength and direction can be understood with the number which is given at the end of an analysis (r).

A positive correlation is one in which the increased value of one variable results in the increased value of another. For example, height and weight – as height increased, weight also tends to increase. A negative correlation is one in which the increased value of one variable results in the decrease of another. For example, as the temperature outside increases, hot chocolate sales will decrease. This is what is meant by the direction of a correlation. An r-value with a negative sign in front of it means a negative correlation and one without a negative sign means a positive correlation. Continue reading →

Statistics: Two-Factor ANOVA

Leave a reply

Introduction to Two-Factor ANOVAs

So far we’ve talked about tests which are used if there is one independent variable, either with two levels or more. This is not the limit of how much we can include in a single analysis. In a two-factor ANOVA, there is more than one independent variable and each of those variables can have two or more levels. Take this example into consideration:

A farmer wants to know the best combination of products to use to maximize her crop yield. She decides to test out three different fertilizer brands (A, B, and C) and two different kinds of seeds (Y and Z). Each product is paired once with another for a total of 6 conditions: AY, BY, CY, AZ, BZ, CZ.

A two-factor ANOVA considers more than one factor and considers the joint impact of factors. This means that instead of running a new study every time you want to see how an independent variable affects a specific dependent variable, you can run an experiment with two different independent variables and seeing how they each impact the dependent variable and you get to see if the two independent variables do anything together to affect the dependent variable. These are called main effects and interactions. Keeping the example going, if we find that no matter what the seed type is that fertilizers A, B, and C resulted in different crop yields from one another, we would say there is a main effect for fertilizer type. If no matter what the fertilizer type is there is a difference between the crop yields of seeds Y and Z, we would say that there is a main effect for seed type. If there are times that the two factors influence each other (for example, let’s say that fertilizer worked much better specifically when paired with Y seeds), we would say there’s an interaction.  The defining characteristic of an interaction is when the effect of one factor depends on the different levels of a second factor or the impact of another factor, either amplifying or reducing the effect based on the level. Continue reading →

Statistics: Repeated Measures ANOVA

Leave a reply

Repeated Measures One-way ANOVA

Just like when we talked about independent samples t-tests and repeated measures t-tests, ANOVAs can have the same distinction. Independent one-way ANOVAs use samples which are in no way related to each other; each sample is completely random, uses different individuals, and those individuals are not paired in any meaningful way. In a repeated measures one-way ANOVA, individuals can be in multiple treatment conditions, be paired with other individuals based on important characteristics, or simply matched based on a relationship to one another (twins, siblings, couples, etc.). What’s important to remember that in a repeated measures one-way ANOVA, we are still given the opportunity to work with multiple levels, not just two like with a t-test.

Advantages:

  • Individual differences among participants do not influence outcomes or influence them very little because everyone is either paired up on important participant characteristics or they are the same person in multiple conditions.
  • A smaller number of subjects needed to test all the treatments.
  • Ability to assess an effect over time.

Continue reading →

Statistics: Independent One-Way ANOVA

Leave a reply

Independent One-way ANOVA

An ANOVA (ANalysis Of VAriance) is a test that is run either to compare multiple independent variables with two or more levels each, or one independent variable with more than 2 levels. You can technically also run an ANOVA in the same cases you would run a t-test and come up with the same results, but this isn’t common practice, as t-tests are easier to compute by hand.

For the purposes of this post, a One-way ANOVA is a test which compares the means of multiple samples (more than 2) which are connected by the same independent variable. An example of this might be comparing the growth of plans who receive no water (Group 1) a little water (Group 2), a moderate amount of water (Group 3), and a lot of water (Group 4).

A factor is another name for an independent variable. As mentioned earlier, ANOVAs can sometimes have more than one factor, but for now we’re only working with one, just like we have before. A level is a group within that independent variable. Using the example from before, the groups in which the plants are put in are the levels (no water, little water, some water, a lot of water) and the independent variable itself is just water amount. Continue reading →

Statistics: Repeated Measures t-test

Leave a reply

Repeated Measures T-Test

A repeated measures or paired samples design is all about minimizing confounding variables like participant characteristics by either using the same person in multiple levels of a factor or pairing participants up in each group based on similar characteristics or relationship and then having them take part in different treatments. Matched subjects is another word used to describe this kind of test and it is used specifically to refer to designs in which different people are matched up by their characteristics. Participants are often matched by age, gender, race, socioeconomic status, or other demographic features, but can also be matched up on other characteristics the researchers might consider possible confounds. Twin studies are a good example of this kind of design; one twin has to be matched up with the other – they can’t be matched to someone else’s twin.

To reiterate the differences between a repeated measures t-test and the other kinds of tests you may have learned up to this point, a single sample t-test revolves around drawing conclusions about a treated population based on a sample mean and an untreated population mean (no standard deviation). An independent sample t-tests are all about comparing the means of two samples (usually a control group/untreated group and a treated group) to draw inferences about how there might be differences between those two groups in the broader population. Different, randomly assigned participants are used in each group. Related samples t-tests are like independent sample t-tests except they use the same person for multiple test groups or they match people based on their characteristics or relationships to cut down on extraneous variables which may interfere with the data. Continue reading →

Statistics: Independent t-tests

Leave a reply

Independent t-test

In our last post, we talked about single sample t-tests, which is a way of comparing the mean of a population with the mean of a sample to look for a difference. With two-sample t-tests, we are now trying to find a difference between two different sample means. More specifically, independent t-tests involve comparing the means of two samples which are distinctly different from one another in regards to the individuals within each sample. For example, a group of pet owners vs. a group of folks who don’t own pets. These two groups are completely independent of one another. This distinction will be important in a later post.

A more technical explanation of the difference between a single sample and two-sample is that a single sample t-test revolves around drawing conclusions about a treated population based on a sample mean and an untreated population mean (no standard deviation). An independent sample t-tests are all about comparing the means of two samples (usually a control group/untreated group and a treated group) to draw inferences about how there might be differences between those two groups in the broader population

There are some distinct advantages and disadvantages to this approach when compared to other approaches. To avoid confusion, we won’t describe the other approaches here but will just mark the advantages and disadvantages of this one here for your consideration: Continue reading →

Statistics: Introduction to the t-statistic

Leave a reply

Introduction to the t-statistic

Z-tests vs. t-tests

Z-tests compare the means between a population and a sample and require information that is usually unavailable about populations, namely the variance/standard deviation. Single sample t-tests compare the population mean to a sample mean, but only require one variance/standard deviation, and that’s from the sample. This is where estimated standard error comes in. It’s used as an estimate of the real standard error, σM, when the value of σ is unknown. It is computed using the sample variance or sample standard deviation and provides an estimate of the standard distance between a sample mean, M, and the population mean, μ, (or rather, the mean of sample means). It’s an “error” because it’s the distance between what the sample mean is and what it would ideally be since we would rather have the population standard deviation. The formula for estimated standard error is s/√n.

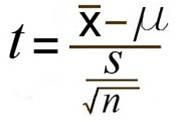The formula for the t-test itself is:   with the bottom portion referring to the estimated standard error. You may see this written as sM instead. Continue reading →

Statistics: Introduction to Hypothesis Testing

Leave a reply

Hypothesis Testing Basics

What is Hypothesis Testing?

Hypothesis testing is a big part of what we would actually consider testing for inferential statistics. It’s a procedure and set of rules that allow us to move from descriptive statistics to make inferences about a population based on sample data. It is a statistical method that uses sample data to evaluate a hypothesis about a population.

This type of test is usually used within the context of research. If we expect to see a difference between a treated and untreated group (in some cases the untreated group is the parameters we know about the population), we expect there to be a difference in the means between the two groups, but that the standard deviation remains the same, as if each individual score has had a value added or subtracted from it. Continue reading →

Statistics: Distribution of Sample Means

Leave a reply

Distribution of Sample Means

Up until this point, as far as distributions go, it’s been about being able to find individual scores on a distribution. Moving into hypothesis testing, we’re going to switch from working with very concrete distributions with scores to hypothetical distributions of sample means. In other words, we’re still working with normal distributions, but the points that make up the distribution will no longer be individual scores, but all possible sample means which can be drawn from a population with a given N or number of scores in them.

We use these kinds of distributions because with inferential statistics we’re going to want to find the probability of acquiring a certain sample mean to see if it’s common or very rare and therefore perhaps significantly different from another mean.

There are some concepts you will have to keep in mind for this shift including sampling error, the central limit theorem, and standard error. Continue reading →