Category Archives: OPRE 315

Statistics: Reading Graphs for Two-Way ANOVAs

Leave a reply

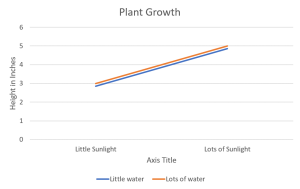
Reading graphs of two-way ANOVAs is often a little frustrating at first for students who are new to reading them. The goal of this post is to hopefully make the process more straight-forward.

If you’re not sure already what a main effect or interaction is, I would suggest heading over to another post about two-way ANOVAs first. The purpose of one of these graphs is to help the reader visualize the results of the test when reading the results can sometimes be overwhelming, especially if the researchers are working with several different levels in each independent variable. The first trick to remember is that when looking for a significant main effect in the variable on the X-axis, we want the mean distance between the two points above one condition to be different from the mean distance between the two points of another condition. A clear example of this is below. The middle point between the orange line and blue line above “Little Sunlight” is around 2.8, while the middle point between the orange line and blue line above “Lots of Sunlight” is about 4.8. Given the context, we would say that there is a main effect for sunlight in which plant growth increases as levels of sunlight increase.

Continue reading →

Statistics: Sampling Distribution of the Proportion

Leave a reply

Sampling Distribution of the Proportion

In this section, we’ll be talking about finding the probability of a sample proportion. You may remember that a sampling distribution is a distribution not of scores, but all possible sample outcomes which can be drawn given that we’re working with a specific n. In this case, the following equations can help us figure out, based on a population proportion, how likely it is that we’ll draw a sample that has a chosen proportion. A question which would require these equations may sound like the following:

“A nation-wide survey was conducted about the perception of a brand. People were asked whether they liked the brand or disliked the brand and the results showed that 65% of people liked the brand. If we were to draw a random sample of 200 people, what is the probability that 80% of people within that sample will say they like the brand?”

The population proportion, denoted as ?, is the proportion of items in the entire population with the particular characteristic that we’re interested in investigating. The sample proportion, denoted by p, is the proportion of items in the sample with the characteristic that we’re interested in investigating. The sample proportion, which by definition is a statistic, is used to estimate the population proportion, which by definition is a parameter. Continue reading →

Statistics: Discrete Probability Distributions

Leave a reply

Introduction to Discrete Probability Distributions

Discrete versus Continuous Variables

A discrete variable typically originates from a counting process while a continuous variable usually comes from a measuring process. An easy way to make the distinction between a discrete and a continuous variable is that discrete variables are usually whole numbers with no decimals. Continuous variables on the other hand frequently take the form of decimals. For instance, the number of people which exist within a group is a discrete variable because it’s always a whole number, while a person’s weight would be continuous since it can typically be measured to multiple decimal places.

The Probability Distribution for a Discrete Variable

A probability distribution for a discrete variable is simply a compilation of all the range of possible outcomes and the probability associated with each possible outcome. Since, probability in general, by definition, must sum to 1, the summation of all the possible outcomes must sum to 1. For example, if you’re flipping a coin once, there’s a 1 in 2 chance it will land on heads, and a 1 in 2 chance it will land on tails; 1/2 + 1/2 = 1. In this way, measuring probability is similar to the use of percentages. Percentages are always measured out of 100 while probability is always measured out of 1. This is true for all probability measurements Continue reading →

Statistics: Choosing a Test

Leave a reply

The following post is about breaking down the uses for different types of tests. More importantly, it’s designed to help you know what test to use based on the question being asked. This is not a comprehensive list of all the statistical tests out there, so if you feel that there is something missing which you would like to be included, please leave a comment below. All formulas for the tests presented here can be found in the Statistics Formula Glossary post. At the bottom is a decision tree which may be helpful in visualizing the purpose of this post. Continue reading →

Statistics Formula Glossary

Leave a reply

Stats Formula Glossary (Word) as of 7/16/2019

Stats Formula Glossary (PDF) as of 7/16/2019

Attached to this post are a PDF version and a Word document version of a glossary of formulas that may be helpful to keep around when practicing statistical problems for homework or studying for an upcoming test.

Please keep in mind that although these formulas work, they may not be the versions that your professors have taught you to use. It may also be that this formula sheet has formulas for problems you don’t need to know how to solve for the purposes of your class. If this is the case, we encourage you to download the Word document version so that you may add to, subtract from, or edit the glossary to fit your own individual needs.

Please keep in mind that this formula sheet may be edited after having been posted; the copy you download today may be different from the copy posted tomorrow. This list is by no means comprehensive of all formulas used in the field of statistics. If you have suggestions on formulas you would like to see added to this list, please leave a comment underneath of this post and we will take your suggestion into consideration. Good luck!

Statistics: Regression

Leave a reply

Introduction to Linear Regression

Linear regression is a method for determining the best-fitting line through a set of data. In a lot of ways, it’s similar to a correlation since things like r and r squared are still used. The one difference is that the purpose of regression is prediction. The best-fitting line is calculated through the minimization of total squared error between the data points and the line.

The equation used for regression is Y = a +bx or some variation of that. If you remember from algebra class, this formula is like Y=mx+b. This is because they are both the linear equation. Although you may be asked to report r and r squared, the purpose of regression is to be able to find values for the slope (b) and the y-intercept (a) that creates a line that best fits through the data. Continue reading →

Statistics: Correlation

Leave a reply

Introduction to Correlation and Regression

So far we’ve been talking about analyses which involve variables which are split up into categorical or discrete variables (ex. treatment A, B, C) compared to a dependent variable which is continuous (ex. plant height). However, there is a way to look at two variables which have continuous data: correlation. A correlation will tell you the characteristics of a relationship such as direction (either positive or negative), form (we often work with linear relationships), and strength of the relationship. Strength and direction can be understood with the number which is given at the end of an analysis (r).

A positive correlation is one in which the increased value of one variable results in the increased value of another. For example, height and weight – as height increased, weight also tends to increase. A negative correlation is one in which the increased value of one variable results in the decrease of another. For example, as the temperature outside increases, hot chocolate sales will decrease. This is what is meant by the direction of a correlation. An r-value with a negative sign in front of it means a negative correlation and one without a negative sign means a positive correlation. Continue reading →

Statistics: Two-Factor ANOVA

Leave a reply

Introduction to Two-Factor ANOVAs

So far we’ve talked about tests which are used if there is one independent variable, either with two levels or more. This is not the limit of how much we can include in a single analysis. In a two-factor ANOVA, there is more than one independent variable and each of those variables can have two or more levels. Take this example into consideration:

A farmer wants to know the best combination of products to use to maximize her crop yield. She decides to test out three different fertilizer brands (A, B, and C) and two different kinds of seeds (Y and Z). Each product is paired once with another for a total of 6 conditions: AY, BY, CY, AZ, BZ, CZ.

A two-factor ANOVA considers more than one factor and considers the joint impact of factors. This means that instead of running a new study every time you want to see how an independent variable affects a specific dependent variable, you can run an experiment with two different independent variables and seeing how they each impact the dependent variable and you get to see if the two independent variables do anything together to affect the dependent variable. These are called main effects and interactions. Keeping the example going, if we find that no matter what the seed type is that fertilizers A, B, and C resulted in different crop yields from one another, we would say there is a main effect for fertilizer type. If no matter what the fertilizer type is there is a difference between the crop yields of seeds Y and Z, we would say that there is a main effect for seed type. If there are times that the two factors influence each other (for example, let’s say that fertilizer worked much better specifically when paired with Y seeds), we would say there’s an interaction.  The defining characteristic of an interaction is when the effect of one factor depends on the different levels of a second factor or the impact of another factor, either amplifying or reducing the effect based on the level. Continue reading →

Statistics: Repeated Measures ANOVA

Leave a reply

Repeated Measures One-way ANOVA

Just like when we talked about independent samples t-tests and repeated measures t-tests, ANOVAs can have the same distinction. Independent one-way ANOVAs use samples which are in no way related to each other; each sample is completely random, uses different individuals, and those individuals are not paired in any meaningful way. In a repeated measures one-way ANOVA, individuals can be in multiple treatment conditions, be paired with other individuals based on important characteristics, or simply matched based on a relationship to one another (twins, siblings, couples, etc.). What’s important to remember that in a repeated measures one-way ANOVA, we are still given the opportunity to work with multiple levels, not just two like with a t-test.

Advantages:

  • Individual differences among participants do not influence outcomes or influence them very little because everyone is either paired up on important participant characteristics or they are the same person in multiple conditions.
  • A smaller number of subjects needed to test all the treatments.
  • Ability to assess an effect over time.

Continue reading →

Statistics: Independent One-Way ANOVA

Leave a reply

Independent One-way ANOVA

An ANOVA (ANalysis Of VAriance) is a test that is run either to compare multiple independent variables with two or more levels each, or one independent variable with more than 2 levels. You can technically also run an ANOVA in the same cases you would run a t-test and come up with the same results, but this isn’t common practice, as t-tests are easier to compute by hand.

For the purposes of this post, a One-way ANOVA is a test which compares the means of multiple samples (more than 2) which are connected by the same independent variable. An example of this might be comparing the growth of plans who receive no water (Group 1) a little water (Group 2), a moderate amount of water (Group 3), and a lot of water (Group 4).

A factor is another name for an independent variable. As mentioned earlier, ANOVAs can sometimes have more than one factor, but for now we’re only working with one, just like we have before. A level is a group within that independent variable. Using the example from before, the groups in which the plants are put in are the levels (no water, little water, some water, a lot of water) and the independent variable itself is just water amount. Continue reading →